coderljw
GitHub (opens new window)

数据结构与算法

coderljw 2024-10-13 数据结构与算法
  • 数据结构与算法
  • 斐波那契数列
  • 排序算法
  • 二分法查找
  • 树形数据结构化
 大约 5 分钟

# 1. 中点

  • mid = L + ((R - L) >> 1)

# 2. 异或运算 ^

  • 无进位相加，0 ^ N等于 N，N ^ N等于 0，满足交换律与结合律。

    0 ^ 7 // => 7
7 ^ 7 // => 0

// 两数交换
let a = 3
let b = 4

a ^= b
b ^= a
a ^= b
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    1. 数列中只有一个数出现奇数次，其余数出现偶数次，求出现奇数次的数？
    const ary = [1, 2, 1, 7, 7, 1, 2, 1, 7]

let num = 0
ary.map(i => (num ^= i))
console.log(num)
    1
    2
    3
    4
    5
    1. 数列中有两个数出现奇数次，其余数出现偶数次，求出现奇数次的数？

    num & (~num + 1) 提取不为零数中最右侧的 1。

    const ary = [1, 2, 1, 7, 7, 1, 2, 1, 7, 9]

let num1 = 0, // num1 = a ^ b，因为 a !== b，所以 num1 !== 0，num1 必然有一位为 1
  num2 = 0 // num2 = a or b
ary.map(i => (num1 ^= i))

let rightOne = num1 & (~num1 + 1) // 取出最右侧的 1
ary.map(i => i & rightOne && (num2 ^= i)) // 划分 a、b，将 a 或 b 赋值给 num2

console.log(num2, num1 ^ num2) // 两数
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

# 3. master 公式

  • 作用：剖析递归行为时间复杂度。

  • T(n)=aT(nb)+O(nd)T(n) = aT(\frac{n}{b}) + O(n^{d})

  1. log(b, a) > d 复杂度为 O(Nlog(b,a))O(N^{log(b, a)})
  2. log(b, a) = d 复杂度为 O(Nd∗logN)O(N^{d} * logN)
  3. log(b, a) < d 复杂度为 O(Nd)O(N^{d})

# 4.斐波那契数列

    1. 递归
    function fibonacci(n) {
  return n < 3 ? 1 : fibonacci(n - 1) + fibonacci(n - 2)
}
    1
    2
    3
    1. 尾调用优化递归
    'use strict'
function fibonacci(n, a = 1, b = 1) {
  return n < 3 ? b : fibonacci(n - 1, b, a + b)
}
    1
    2
    3
    4
    1. 循环
    function fibonacci(n) {
  if (n < 3) return 1
  let ary = [1, 1]
  let i = n + 1 - 2
  while (i > 1) {
    const [a, b] = [ary[ary.length - 2], ary[ary.length - 1]]
    ary.push(a + b)
    i--
  }
  return ary.at(-1) // ary.slice(-1)[0]
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11

# 5. 排序算法

  • 1.1 传统冒泡排序

    function bubbleSort(ary) {
  const len = ary.length

  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      // 相邻元素两两对比
      if (ary[j] > ary[j + 1]) {
        ;[ary[j], ary[j + 1]] = [ary[j + 1], ary[j]]
      }
    }
  }

  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14

  • 1.2 改进冒泡排序

    设置一标志性变量 pos，用于记录每趟排序中最后一次进行交换的位置。由于 pos 位置之后的记录均已交换到位，故在进行下一趟排序时只要扫描到 pos 位置即可。

    function bubbleSort(ary) {
  let i = ary.length - 1 // 初始时，最后位置保持不变
  while (i > 0) {
    let pos = 0 // 每趟开始时，无记录交换
    for (let j = 0; j < i; j++)
      if (ary[j] > ary[j + 1]) {
        pos = j // 记录交换的位置
        ;[ary[j], ary[j + 1]] = [ary[j + 1], ary[j]]
      }
    i = pos // 记录下趟排序截止位置
  }
  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    1. 选择排序
    function selectionSort(ary) {
  let len = ary.length
  let minIndex
  for (let i = 0; i < len - 1; i++) {
    minIndex = i
    for (let j = i + 1; j < len; j++) {
      // 寻找最小的数，将最小数的索引保存
      if (ary[j] < ary[minIndex]) minIndex = j
    }
    ;[ary[i], ary[minIndex]] = [ary[minIndex], ary[i]]
  }
  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13

  • 3.1 传统插入排序

    function insertionSort(ary) {
  for (let i = 1; i < ary.length; i++) {
    const key = ary[i]
    let j = i - 1
    // 依次与已排序数组比较
    while (j >= 0 && ary[j] > key) {
      ary[j + 1] = ary[j]
      j--
    }
    ary[j + 1] = key
  }
  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13

  • 3.2 改进插入排序

    查找插入位置时使用二分查找的方式

    function insertionSort(ary) {
  for (let i = 1; i < ary.length; i++) {
    const key = ary[i]
    // 二分法查找
    let L = 0,
      R = i - 1
    while (L <= R) {
      let mid = L + ((R - L) >> 1)
      if (key < ary[mid]) R = mid - 1
      else L = mid + 1
    }

    for (let j = i - 1; j >= L; j--) ary[j + 1] = ary[j]
    ary[L] = key
  }
  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    1. 希尔排序
    function shellSort(ary) {
  const len = ary.length
  let temp = 1
  let gap = 1

  // 动态定义间隔序列
  while (gap < len / 5) gap = gap * 5 + 1
  for (gap; gap > 0; gap = Math.floor(gap / 5)) {
    // 插入排序
    for (let i = gap; i < len; i++) {
      temp = ary[i]
      let j = i - gap
      for (; j >= 0 && ary[j] > temp; j -= gap) {
        ary[j + gap] = ary[j]
      }
      ary[j + gap] = temp
    }
  }
  return ary
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    1. 归并排序
    function mergeSort(ary) {
  // 采用自上而下的递归方法
  const len = ary.length
  if (len < 2) return ary
  const mid = len >> 1,
    left = ary.slice(0, mid),
    right = ary.slice(mid)
  return merge(mergeSort(left), mergeSort(right))
}

function merge(left, right) {
  const res = []
  while (left.length && right.length) {
    if (left[0] <= right[0]) res.push(left.shift())
    else res.push(right.shift())
  }
  while (left.length) res.push(left.shift())
  while (right.length) res.push(right.shift())
  return res
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    1. 快速排序
    function quickSort(ary) {
  const len = ary.length
  if (len < 2) return ary
  // 找基准，并把基准从原数组删除保存在变量pivot
  const pivotIndex = len >> 1
  const pivot = ary.splice(pivotIndex, 1)[0]
  // 定义左右数组
  const left = [],
    right = []
  // 比基准小的放在left，比基准大的放在right
  for (let i = 0; i < ary.length; i++) {
    if (ary[i] <= pivot) left.push(ary[i])
    else right.push(ary[i])
  }
  // 拼接数组并分别递归
  return quickSort(left).concat([pivot], quickSort(right))
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    1. 堆排序
    function heapSort(ary) {
  // 建堆
  let heapSize = ary.length
  for (let i = (heapSize >> 1) - 1; i >= 0; i--) {
    heapify(ary, i, heapSize)
  }
  // 排序
  for (let j = heapSize - 1; j >= 1; j--) {
    ;[ary[0], ary[j]] = [ary[j], ary[0]]
    heapify(ary, 0, --heapSize)
  }
  return ary
}

function heapify(ary, x, len) {
  const L = 2 * x + 1
  const R = 2 * x + 2
  let largest = x
  if (L < len && ary[L] > ary[largest]) largest = L
  if (R < len && ary[R] > ary[largest]) largest = R
  if (largest !== x) {
    ;[ary[x], ary[largest]] = [ary[largest], ary[x]]
    heapify(ary, largest, len)
  }
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
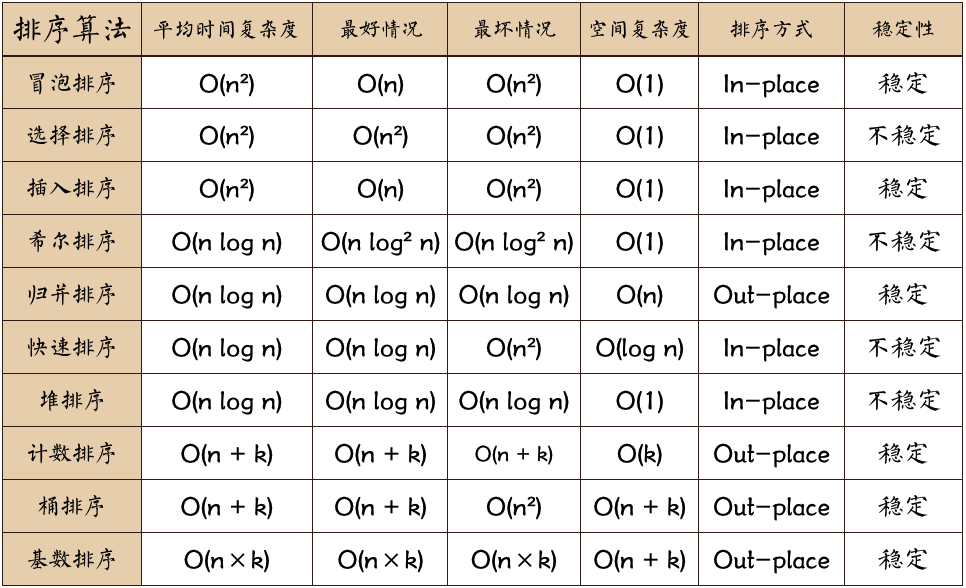
    25

  • 十大经典排序算法总结 - Damonare (opens new window)

# 6. 二分法查找

function binarySearch(ary, target) {
  let L = 0
  let R = ary.length

  while (L <= R) {
    let mid = L + ((R - L) >> 1)
    if (target === ary[mid]) return mid
    else if (target < ary[mid]) R = mid - 1
    else L = mid + 1
  }

  return -1
}
1
2
3
4
5
6
7
8
9
10
11
12
13

# 7. 树形数据结构化

const ary = [
  {
    id: 1,
    pid: 0,
    title: 'jack',
  },
  {
    id: 2,
    pid: 0,
    title: 'pony',
  },
  {
    id: 3,
    pid: 1,
    title: 'Evan You',
  },
  {
    id: 4,
    pid: 3,
    title: 'coderljw',
  },
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
    1. 递归
function formatDataTree(ary) {
  const parents = ary.filter(p => p.pid === 0)
  const children = ary.filter(c => c.pid !== 0)

  aryToTree(parents, children)
  return parents

  function aryToTree(parents, children) {
    parents.map(p => {
      children.forEach((c, i) => {
        if (p.id === c.pid) {
          if (p.children) p.children.push(c)
          else p.children = [c]
          aryToTree(p.children, children)
        }
      })
    })
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
    1. 扁平化处理
const tree = ary.filter(p => {
  const children = ary.filter(c => p.id === c.pid)
  children.length && (p.children = children)
  return p.pid === 0
})
1
2
3
4
5

以父之名
周杰伦.mp3